H30裁判所職員
A〜Hの文字が書かれた8枚のコインを図のように円周上に並べる。いま, Aから順に1,2,3……と右回りに数え始め, 7番目であるGを取り除く。次にGの次のHから順に1,2,3……と数え始め,7番目であるFを取り除く。同様にして,次はHから数え始めて7番目のHを取り除く。こうして次々に7番目のコインを取り除いていくと,最後は1枚だけコインが残ることになる。こうした操作について,次のことが言える。
ア 最後にAを残すには, X(A〜Hのいずれか)から数え始めればよい。
イ 最後にアで定めたXを残すには,Y(A〜Hのいずれか)から数え始めればよい。
このとき,Yに該当するコインとして,正しいものはどれか。
1. A
2. B
3. C
4. D
5. E
※
本問は「操作手順」の問題に分類されます(継子立て、ヨセフスの問題と呼ばれる問題です)。
数学パズルが好きな方は知っているかもしれませんが、このような設定の問題を初めて見たという人も多いでしょう。
このような「操作手順」の問題に対してはポイントがあります。
「ひたすら書き出すことで解けそうかどうか」です。
見たことがないから手を付けないという人もいますが、ぜひ、次のように分類するようにしてみましょう。
(1)どこからアプローチすればよいかわからない問題。
(2)手間はかかりそうだけど、書き出せば解けそうな問題。
(1)は「難しい問題」、(2)は「面倒くさい」問題と考えるようにと私は授業で話しています。
「難しい問題」は、気づけばあっさり解けるかもしれませんが、解くのにどれだけ時間がかかるかわかりません。
一方「面倒くさい問題」は、2種類に分類できます。(2−1)解き方はわかるけど書き出したら何十分もかかりそうな問題、(2−2)そこまで時間を取られずに書き出せそうな問題です。
(2−1)は出題者の立場からすると、「こんな面倒なんだから、何か工夫を考えてね」というメッセージで、「規則性」を見つける問題が多いです。
(2−2)は多少時間はかかるかもしれませんが、確実に作業を行えば、正解できる問題です。
本問はどれに分類されるでしょうか。問題文で途中まで方法が書いてありますし、コインは8枚しかありません。(2−2)と考えることができるでしょう。もしこれが100枚のコインとなれば、(2−1)です。
判断推理の「操作手順」や数的推理の「規則性」の問題では、(2−2)のような問題は、しっかりと点数に結びつけましょう。このような視点で取捨選択を考え、解くべき問題と切るべき問題を選別できるようにしましょう。
本問は、Aから順にひたすらコインを取り除いていけば、多少面倒ではありますが、最後の1枚を判別することができそうです。
例えば、Aから始めて最後にAが残れば、最初に選んだコインが最後まで残るとわかります。
もし、Aから始めて、Cが残れば、最初に選んだコインの2つ先が残ることがわかります。
いずれか1枚のコイン(今回はA)で試せば、どのコインから始める場合についても、対応できそうです。
それでは、そろそろ解説をしていきましょう。
このような問題であっても、図表を活用し、状況把握をすることが重要です。
7番目のコインを取り除くことから、図のように、1から7の数字を振って、AからHの順に並べていくと良いでしょう。
最初は図のようにGが取り除かれ、Hが次の1番目のコインになります。取り除いたコインもわかるにしましょう。

その後、2番目にA、3番目にBと続き、7番目のFが取り除かれ、Gは既に取り除かれているので、Hが次の1番目になります。

同様に繰り返していくと、以下のようになります。

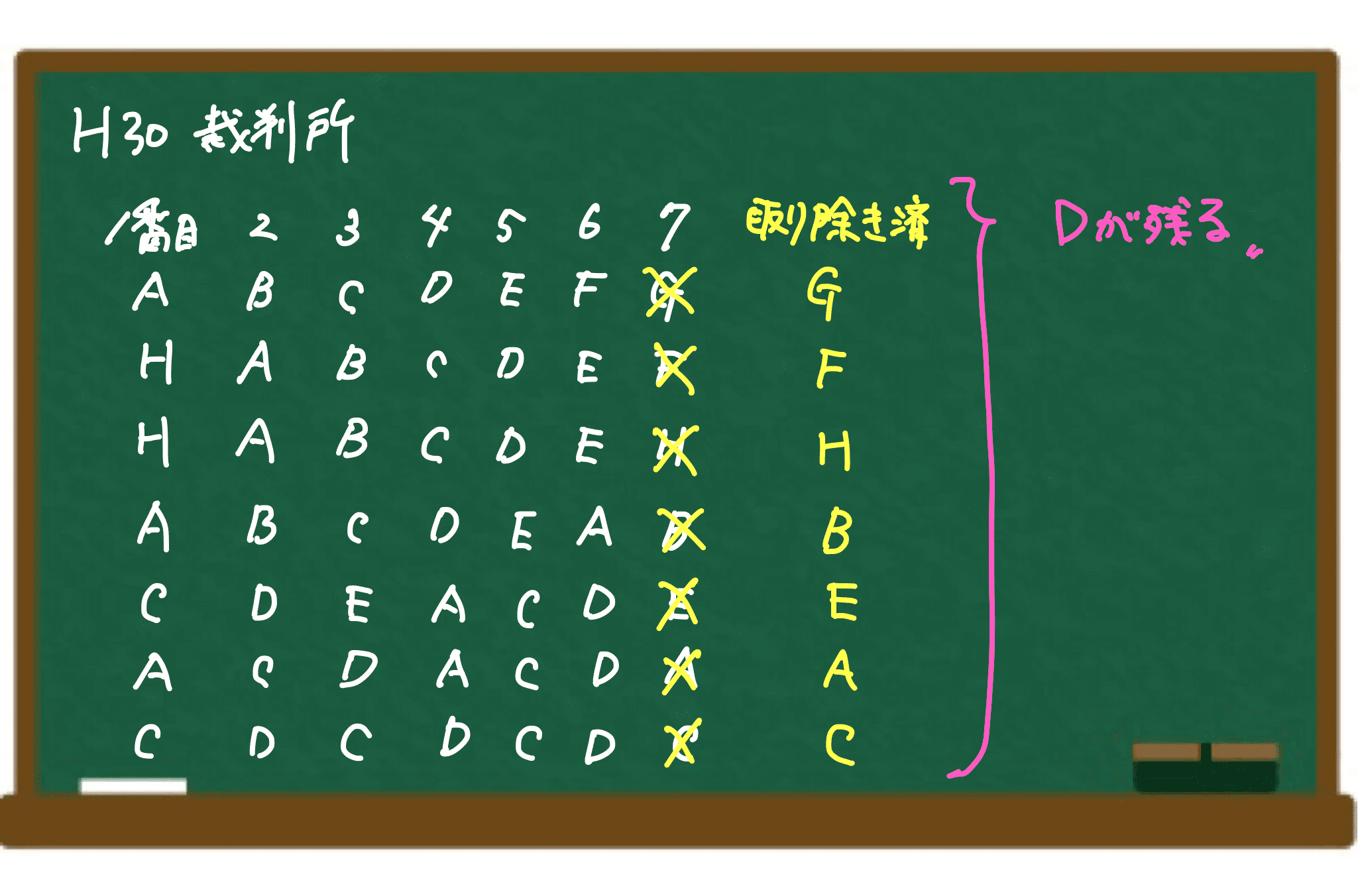
以上より、Aから始めると3つ先のDが残ることがわかります。
問題文のア、イは、最後に残したいコインがわかっていて、始まりがどのコインかを考える設定です。
慎重に図を描いてみれば、XやYを残したいときには、その3つ前から始めればよいことがわかります。
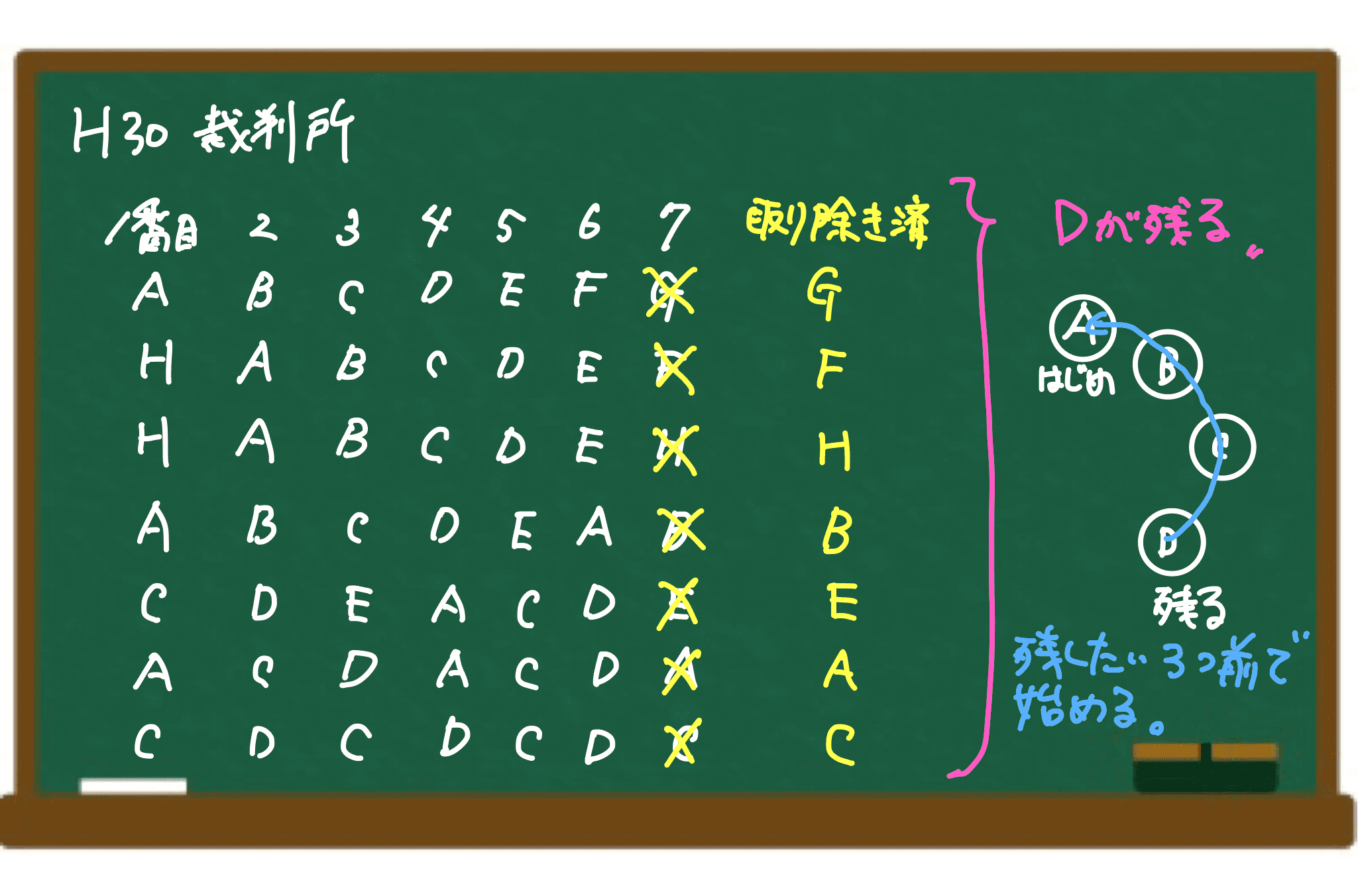
よって、アのAを残すには3つ手前のF(X)から始め、イのF(X)を残すには3つ手前のC(Y)から始めればよいことがわかります。
[正解3]
本試験では、今まで勉強してきた中で「見たことがない」問題も当たり前のように出題されます。そのような問題の取捨選択は重要なポイントです。
本問のような問題に限らず、解くべきか、切るべきかを判断する力は、日頃から意識して磨いておきましょう。
※
電子書籍の新刊を執筆中です。次は『場合の数』についてです。解説する問題の選定とプロットも決まりました。比較的よく出題されるパターンものが完璧に解けるようになってもらえるよう、しっかりと解説の仕方を考えていきたいところです。何とか年始あたりに出せればと思っています。
以下は既刊についてのリンクです。
